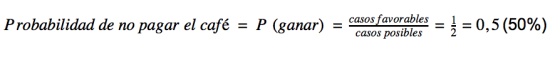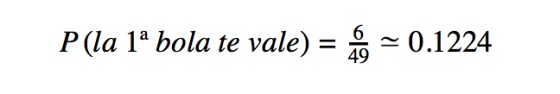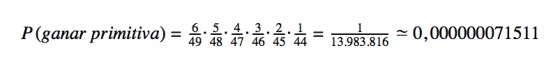Periódicamente oímos hablar de botes millonarios en el sorteo de La Primitiva, del Euromillones, de la Quiniela y nos decimos eso de ¿y si me toca? El bote de La Primitiva de esta semana es uno de los mayores en la historia del sorteo.
Si te toca, podrás reírte de aquel de los Donettes, al que le salían amigos por todas partes. Incluso podrás encontrar empresas especializadas en gestionar tu fortuna. Pero pongámonos serios: ¿qué posibilidades reales hay de que te toque? Mejor aún, ¿cuál es la probabilidad de que te toque?
El cálculo de probabilidad cuando nos encontramos en un experimento simple es sencillo: divides el número de casos a tu favor entre el número de casos posibles que haya. Un ejemplo, me juego contigo a cara o cruz quién paga el café:
Favorable es que salga lo que yo quiero, posible es que salga cara o cruz -porque las monedas casi nunca caen de canto-. Si al día siguiente repetimos el experimento obtendremos ese mismo 0,5 que se corresponde con el 50% de veces que esperamos que nos toque pagar (a la larga nos igualaremos ¿no?).
Si nos jugamos que me invites hoy y mañana tendremos que multiplicar la probabilidad de que me invites hoy por la de que me invites mañana, ya que son dos sucesos independientes -hasta que empieces a sospechar-. Observa que puede salir CC (cara y cara), CX (cara y cruz), XC (cruz y cara) y XX (cruz y cruz) siendo todos igual de probables. Cada uno tiene una probabilidad de 0,25 (que es lo mismo que si multiplicas 0,5 por 0,5).
Imagina que has comprado un boleto de la Primitiva, has rellenado los seis números y estás esperando ver salir -no importa el orden- tus seis bolas entre las 49 que tiene el bombo. Como las extracciones se hacen una detrás de la otra no se repite el mismo número de casos favorables y casos posibles, porque son sucesos dependientes. Pero sí que se repite la misma operación de multiplicar. Para la primera extracción podrían sacar cualquiera de “tus bolas”, por tanto la probabilidad de que esta primera extracción te sea favorable es:
O sea, que puedes pensar que en el 12% de los sorteos la primera bola va a estar en tu boleto. No es mucho, pero tampoco está mal.
Ahora necesitas que la segunda también esté en tu boleto:
En este caso, solo hay 5 números favorables, porque ya hemos gastado uno, y solo quedan 48 en el bombo, pero vamos bien. Ahora es como el café de antes, si necesitas que en tu boleto estén los dos números que han salido te toca multiplicar los dos números decimales, estas dos probabilidades.
Obtienes un exiguo 0,0128, si lo pasamos a tanto por ciento, solo tienes el 1,28% de probabilidades de tener esas dos primeras bolas en tu boleto. Poco más que una de cada cien. No olvides que cuando se multiplican dos números entre 0 y 1 el resultado se va haciendo más pequeño cada vez.
Si sigo este proceso -que te voy a ahorrar- la probabilidad de que alguien tengan los seis números en el sorteo de la Primitiva es:
Pero esto no es todo. Para conseguir el premio máximo hay que tener, además, el reintegro. El reintegro es un número del 0 al 9, lo que multiplicaría la probabilidad anterior por 1/10 (o 0,1). Es decir, la probabilidad final de tener los seis números y el reintegro es de 0,0000000071511.
El número anterior es muy pequeño, aproximadamente uno entre 140 millones. ¿Quiere decir esto que si compras 140 millones de boletos para el mismo sorteo te toca sí o sí?. En efecto, y no sería la primera vez. El problema lo vas a encontrar a la hora de rellenar los 140 millones de boletos y al adelantarle al estado 140 millones de euros. El otro problema será que nada te garantiza que el bote completo sea para ti. Tal vez salga una combinación muy popular, por ejemplo 4, 8, 15, 16, 23 y 42 y te toque repartir el bote entre una legión de fanáticos de Lost.
Esto que acabamos de decir tiene una derivada importante, pensando en ganar el bote (o sea, en ser el único acertante) es mejor jugar una combinación “difícil”. Por ejemplo, una que no se corresponda con los cumpleaños de los hijos de nadie (los niños no nacen los días 34 o 72) porque es más probable que nadie la haya elegido. Así que sí, hay combinaciones mejores que otras para llevarse el bote íntegro (aunque todas tengan la misma probabilidad), pero no es gracias a las matemáticas sino a que la gente juega números que les son familiares.
¿Y los otros sorteos?
El más llamativo y mediático -por sus botes estratosféricos- es el sorteo del euromillón, pero no te aconsejo intentar comprar todos los boletos. Las combinaciones posibles son 116.531.800, todo un número grande.
La quiniela no es un sorteo, porque el resultado de los partidos no se corresponde con el azar. Pero jugar a la quiniela al azar, genera algo más que 14 millones de combinaciones diferentes puesto que cada uno de los 15 partidos que se consideran puede ser 1, X ó 2 (gana local, empatan, gana visitante) y eso se traduce en 3·3·3...·3 (quince veces), 14.348.907 posibles resultados.
Los sorteos del cupón de la ONCE se hacen entre 100.000 números (los que van del 00000 -se lee “cero”- al 99.999) por lo que parecen más probables. Pero si quieres llevarte el premio gordo tienes que acertar también la serie (y hay 150) el resultado de considerar todos los números con todas sus posibles series nos deja un total de 15 millones de cupones distintos… parece que todo anda por los quince millones.
¿Y los rascas? En los sorteos de rascar en los que no hay bolas girando en bombos la cosa se complica. La empresa que realiza el sorteo debe controlar que no se dan más premios que los que tiene previsto, por lo que puede ocurrir que sepan cuáles son los tickets premiados. El único azar aquí es que tú -incauto pagador de este impuesto que pagan los que no saben de matemáticas- encuentres el rasca que tiene el premio.
No descartemos que, tras un concienzudo análisis de la infinidad de sorteos que hay en el planeta, puedas descubrir que no es un verdadero sorteo. Pero siempre puedes beneficiarte de ello (como estos pollos) o comunicárselo al organismo gestor, como hizo este buen ciudadano.
Y una cosa importante: si te toca el premio, no olvides cobrarlo.
* También puedes seguirnos en Instagram y Flipboard. ¡No te pierdas lo mejor de Verne!