La próxima vez que oigas que los matemáticos no saben bailar ya sabrás que no es así, es solo que están pensando en las matemáticas que hay detrás de cada paso, y tratando de hacerlo de manera matemáticamente correcta.
El otro día me llegó este vídeo a lo mejor lo has visto, según Facebook lleva más de 30 millones de reproducciones:
La verdad es que es curioso, la música es pegadiza -aunque no tanto como el himno del PP en versión latina- y el monigote de stick figure, tan utilizado para divulgar ciencia, es cachondo. Es un meme antiguo que en forma de imagen se comparte al menos desde 2012 y que puedes incluso encontrar en camisetas. Por supuesto, hay gif.
Como tantos otros chistes matemáticos, tiene una componente un tanto hermética que me gustaría explicar. Luego está el otro asunto que también debo comentar, y es que, después de 30 millones de veces visto el vídeo y muchos más la imagen, tengo que confesar que está mal -no está fatal, seguro que se puede aprobar-, pero no tiene el rigor que se espera de las matemáticas.
Cuando los matemáticos hablamos de función nos estamos refiriendo generalmente a una relación entre dos conjuntos de números (números reales, en primaria y secundaria). Esa relación puede venir dada de varias formas, en el caso más típico a través de alguna de estas tres: una tabla, una gráfica o de una expresión algebraica.
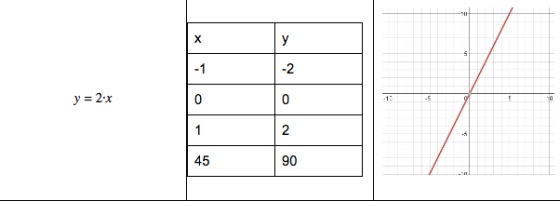
Entrando en el detalle de las funciones que baila nuestro monigote nos encontramos algunas de las más conocidas de las clases de mates y también podremos entender cómo se elabora la tabla o la gráfica.
La identidad: y = x
Es una función muy curiosa, no cambia nada, o sea, que la y vale exactamente lo mismo que la x. Su tabla contendría dos columnas idénticas. La gráfica si disponemos de tabla se elabora marcando en unos ejes de coordenadas los puntos que encontramos en ella. En este caso sería una línea recta que pasa por puntos que tienen sus dos coordenadas iguales, tanto su x (abcisa o coordenada horizontal) como su y (ordenada o coordenada vertical). Es decir, que están tan alejados del origen de coordenadas hacia los lados como en vertical.
La siguiente es la función opuesta, que cambia el signo. Si te imaginas las funciones como una máquina de cambiar cosas, esta es la función que le cambia el signo a los números, si entra el 5, sale el -5, si entra el -π sale π, si entra el 0, sale también el 0 (pasa por el origen).
Valor absoluto: y = |x|
Esta función le quita el signo a los números, si son negativos o positivos da igual, valen lo alejados que estén del 0. Si quieres ver su gráfica se lo puedes preguntar directamente a Google, pero diciéndole y = abs (x). Tiene forma de V, y si le preguntamos por su opuesta, pues de V invertida. Como los números que están a la misma distancia del origen van al mismo destino (tanto el 5 como el -5 van por esta función al 5) decimos que esta función es simétrica par.
Parábola
En aquellos días, estaba Jesús con sus discípulos:
-En verdad os digo, y igual x al cuadrado.
-¿Eso que es, maestro?
-Una parábola.
No me digas que no se merece un lugar entre los mejores peores chistes.
La función asigna a cada número su cuadrado, por eso tiene los dos brazos para arriba, porque los cuadrados de los números son todos positivos. Sobre la gráfica, dando por bueno lo del cuello y el origen de coordenadas, sí que parece una parábola.
La función cúbica lleva cada número a ese mismo número multiplicado por sí mismo tres veces, o sea, que deja fijos -1, 0 y 1 pero manda el 2 al 8 y el 10 al 1000, como manda el -2 al -8 decimos que es una función simétrica impar o respecto del origen de coordenadas.
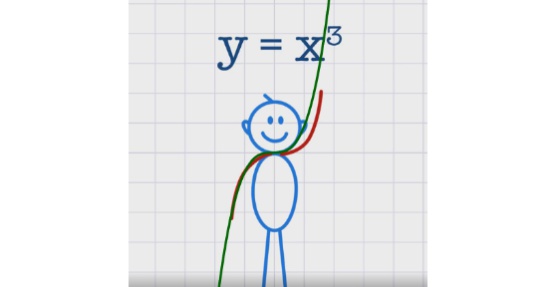
Función inversa y = 1/x
Se llama hipérbola y no te voy a contar ningún chiste sobre ella. Si la fórmula no te resulta suficientemente transparente, lo que hace esta máquina es transformar cada número en su inverso, en uno dividido por ese número. Por eso llevará el 2 a ½, 0,5, el tres a un tercio y el diez a un décimo. Eso se traduce en que la imagen del mil es 0,001 y que cada vez los brazos serán más cercanos a la línea horizontal, aunque sin llegar a tocarla, eso recibe el nombre en matemáticas de asíntota horizontal y no es la única que tiene porque los números muy próximos al cero al invertirse crecen muy rápidamente, generando una asíntota vertical (esa es otra explicación de por qué al dividir por un número entre -1 y 1 da un resultado mayor que el dividendo). Esto es un problema a la hora de dibujar a nuestro muñeco porque no es que no pase por el origen de coordenadas, es que no hay nada sobre el origen de coordenadas.
Lleva cuidado si intentas hacer la imagen de la izquierda con tus brazos, más aún si haces la de la derecha que está sacada con Wolfram Alpha, un motor de conocimiento computacional increíble.
Logaritmo: y = log ax
El logaritmo, explicado en pocas palabras, es preguntarse qué exponente tendría x si lo escribiésemos como potencia de base a. Por concretar un poco: en base 10 el logaritmo de 100 es 2 porque el exponente al que hay que elevar 10 para que resulte 100 es 2. Si tomamos un gúgol, que es un número bastante grande, su logaritmo es 100, porque 10 elevado a 100 es precisamente un googol.

Exponencial: y = a^x (^ es la forma de poner exponentes en Internet). Significa a multiplicada por sí misma x veces, asi que primero tendremos que elegir una a. Vamos a tomar a = 2 y x un número natural.

La gráfica no está mal del todo:
El seno (y el coseno) y = sen x
En castellano se dice seno (y tiene algún chiste malo). En inglés utilizan el cultismo sinus, que abreviado “sin” suena a pecado. Son funciones trigonométricas que ya te contaré otro día, pero que tienen la forma de onda que ha dibujado con más o menos acierto nuestro monigote:
La circunferencia
No es preciso que te explique la forma que tiene, observa que es la única que no aparece la “y” despejada al otro lado del igual, la razón es que ¡no es una función! (Aunque nadie dijo que tuvieran que serlo). Si nos movemos en el ancho de su diámetro horizontal encontraremos que hay dos íes griegas para cada x, no podemos hacer una tabla porque cada valor de la x tiene que tener dos valores de y (imágenes) y eso rompe la condición de ser función:
* También puedes seguirnos en Instagram y Flipboard. ¡No te pierdas lo mejor de Verne!










