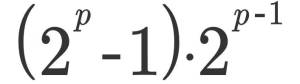Alguno habréis leído que unos matemáticos han descubierto un número primo muy grande. Pertenece a una familia muy especial de números primos, que es la de los primos de Mersenne. Son unos números muy particulares, si quieres encontrar un primo de Mersenne te dejo el siguiente algoritmo. La receta:
1. Se toma un número primo (llamémosle p).
2. Elevas dos al número p, o sea, lo multiplicas por sí mismo p veces.
3. Le restas uno al resultado de 2.
4. Si el resultado es un número primo, ¡BINGO!, es un primo de Mersenne
Veamos un ejemplo. Tomas el primer primo que hay, 2. Elevas dos “al cuadrado”, dos por sí mismo dos veces, 2·2, te da 4. Le restas 1, te da 3. ¡Es primo! Pues entonces es un primo de Mersenne. Te recuerdo que un número es primo si solo se puede dividir por uno y por sí mismo.
Esta familia de primos se conocía desde la antigüedad, pero solo se sabía de los cuatro primeros (3, 7, 31 y 127). De hecho, cuando se descubrió el quinto (en el siglo XV) se llegó a formular que todos los números que salían de hacer los pasos de 1 a 3 resultaban número primo partiendo de cualquier número primo p.
La familia fue creciendo según mejoraban las técnicas de cálculo y llegó a tener 12 primos en el siglo XIX. Luego creció más con la introducción de las computadoras en los años 50 del siglo pasado.
El que se ha anunciado en enero de 2016 es el cuadragésimo noveno primo de Mersenne. 49 primos. Añado que nuestro primo (que se obtiene cuando elevamos dos a 74.207.281 y le restamos uno) tiene 22 millones de cifras (empieza por 300376418… y termina mucho después). Puede que me digas aquello de “¿a mí qué tu primo?”.
Ten en cuenta que muchos de los sistemas que encriptan mensajes a través de redes se apoya en la factorización de números grandes. Esto es, yo puedo cifrar los mensajes gracias a que conozco la factorización de un número bastante grande. Es un número que parece primo, pero que no lo es: tiene factores que yo conozco. Las técnicas para factorizar ese número que hay hoy en día en el mercado toman mucho tiempo (más que el que lleva girando la Tierra alrededor del Sol). Si los malos supieran factorizar cualquier número grande en un periodo razonable de tiempo, adiós seguridad en la red.
Por eso, fundamentalmente, es importante mantener engrasada la máquina de factorizar números así como los algoritmos que proporcionan primos grandes. O sea que la pelea por obtener primos grandes -además de una lucha por ver quién tiene la lista más larga- tiene una gran utilidad práctica.
La búsqueda de primos de Mersenne tiene una derivada mucho menos prosaica: el descubrimiento de nuevos números perfectos. Un número perfecto es aquel en el que la suma de sus divisores propios (excluyendo el número) suman el propio número. Los griegos decían "el que es igual a la suma de sus partes". Se tomaron la molestia de ponerles nombre y eso que solo conocían cuatro. El primer número perfecto es 6, tiene 3 divisores si excluimos al propio número: 1, 2 y 3. Si los sumamos 1 + 2 + 3 = 6. Seis es perfecto, ya lo sospechabas, seguro. El siguiente es 28. Es divisible entre 1 (siempre), 2, 4, 7 y 14 ¿adivinas cuánto da 1 + 2 + 4 + 7 + 14? Exacto, 28.
Cada primo de Mersenne va acompañado de un número perfecto par. Si “2 elevado a p - 1” es primo (y por tanto primo de Mersenne) entonces es perfecto el resultante de:
Vamos a usar la fórmula para encontrar el tercer número perfecto. Para p=5, dos elevado a 5 es 32, 31 es primo entonces 31·16 = 496 es un número perfecto. Multiplico por 16 porque el segundo factor de la fórmula me pide multiplicar por dos elevado a p menos uno, en nuestro caso 2 a la cuarta potencia, 16.
6, 28, 496. Te voy a dar uno más: 8128, que además de la contraseña de mi iPad (voy a tener que cambiarla) es el producto de 127 (primo de Mersenne) por 64. Te dejo como ejercicio que encuentres los siguientes 45 números perfectos.
* Para que no te pierdas nada, nosotros te mandamos lo mejor de Verne a tu móvil: ¡únete a nuestro Telegram telegram.me/verneelpais!
* También puedes seguirnos en Instagram y Flipboard. ¡No te pierdas lo mejor de Verne!