Los acertijos matemáticos del falso inventor del parchís

Hoax, bulo en inglés, es un término que se ha popularizado en estos últimos años porque se utiliza, precisamente, para los bulos que circulan por internet. Seguro que te habrá llegado alguno y que los habrás desmentido aquí en Verne tenemos nuestro propio Tragabulos y los perseguimos (y disfrutamos) con pasión. Por eso hablando de juegos matemáticos que puedes hacer tú mismo había que darle un espacio al mayor inventor de fake news matemáticas, Sam Loyd.

Loyd nació en 1841 y aunque empezó a estudiar para ingeniero lo cambió por el ajedrez. Dicen que no se le daba mal: publicó su primer problema de ajedrez a los 14 años y fue autor de varias columnas en prensa especializada sobre el juego. Podemos encontrar en las notas biográficas de su compañía que llegó a ser el decimoquinto mejor jugador del mundo. No lo vamos a dudar, pero, claro, en su tarjeta de visita también se presentaba como inventor del “Parchessi”, sí el parchís, el que inventaron los indios en el siglo XVI.

También dice que inventó el puzle del 15. El juego consistía en ir moviendo piezas numeradas del uno al 15 en un tablero con 16 espacios en el que quedaba uno libre, con el objetivo de que el 14 y el 15 quedaran en orden correcto.

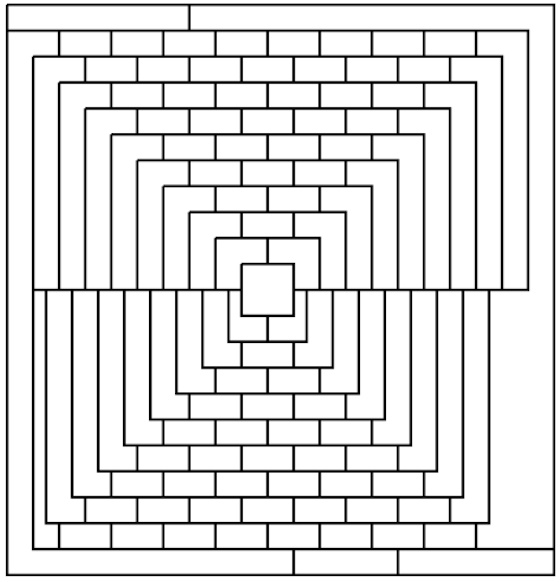
Sobre el juego del 15, ¿verdad que recuerda a nuestros puzles laberinto? (si eres un xennial puede que no entiendas el anterior enlace). Antes de que te vengas arriba y te pongas a resolverlo, hay dos observaciones. La primera es que no es suyo, sino que lo inventó Matthias Rice 12 años antes de la primera vez que Loyd se lo atribuyera y alcanzó muchísima popularidad, sirviendo incluso para viñetas de sátira política, como se puede ver en el artículo (en inglés) del historiador Jerry Slocum en el que desmonta esta y otras atribuciones de Loyd.

La segunda es que cuando decimos que el 14 y 15 queden en “orden correcto” estamos simplificando el juego original. En él, el espacio libre debía quedar abajo a la derecha del 15, pero en la “versión” de Loyd solo se hablaba de colocar la secuencia en orden correcto (sin levantar las fichas, claro). La diferencia es notable: el pasatiempo original no tenía solución, la variante de Loyd, sí.

Lo curioso es que a él este detalle se le pasó por alto, ya que cuando publicó el reto en The illustrated american en 1896 ofreció una recompensa de 1.000 dólares para quien lo lograse resolver, una recompensa que no pagó... porque le llegaron demasiadas soluciones. Así que ahí va nuestro primer reto: da una solución al puzle del 15 y explica los movimientos que conducen a ella. Eso sí, no esperes ni un euro de premio.

Al parecer, Loyd sí que es el creador del reto de Klondike, un puzle en el que partiendo de la posición central puedes caminar en cualquier línea recta (vertical, horizontal o diagonal) tantos pasos como el número en el que hubieras caído. El objetivo es ir un paso más allá de la frontera. Este puzle le gustaba especialmente, ya que a diferencia de los laberintos a los que jugábamos de pequeños, es imposible empezar por el final.

Loyd contribuyó a la difusión de retos famosos divulgando, por ejemplo, esta curiosa variante del conocido problema del lobo la oveja y la col.

Las cuatro fugas

En algún momento del siglo pasado, a juzgar por sus ropajes, cuatro solteros celosos se fugaron con sus también celosas amadas (insistimos: el acertijo es del siglo pasado). En su huida se vieron forzados a cruzar un río caudaloso en un bote que solo podía -una vez más- acarrear a dos personas por viaje. En mitad de la corriente, tal como muestra la ilustración, había una pequeña isla.

Parece que los jóvenes eran tan celosos que ninguno de ellos permitía que su futura esposa permaneciera ni un segundo en compañía de otro hombre u hombres a menos que también él estuviese presente. Y ninguno de ellos estaba dispuesto a embarcarse solo en el bote cuando hubiera una muchacha sola, en la isla o en la costa, si esta muchacha no era aquella con la que estaba comprometido. Esto confirma que ellas también eran celosas, ya que temían que sus compañeros huyeran con alguna de las otras si se les daba la oportunidad. Así las cosas, el problema consiste en descubrir cuál es la manera más rápida de hacer cruzar el río a todo el grupo.

¿Cuántos viajes debe hacer el bote para cruzar a todas las parejas según las condiciones impuestas? La solución del mínimo número de viajes la puedes encontrar en el libro Mathematical Puzzles of Sam Loyd, editado por Martin Gardner en 1959 y si no puedes esperar a recibirlo, ve al final del artículo.

La solución que propone Gardner también era la favorita de Henry Dudeney, un matemático inglés creador de juegos y puzles, que mantuvo una correspondencia muy activa con Loyd, hasta que descubrió que su correspondiente se dedicaba a atribuirse y registrar las ideas que él compartía.

Martin Gardner, que creó y popularizó cientos de problemas matemáticos -suyos y de otros- también hizo sus pinitos en esto de los bulos. Como conté en una ocasión, propuso un “contraejemplo” al teorema de los cuatro colores, en la época en la que aún era una hipótesis, o sea que no estaba demostrado. El teorema establece que cuatro colores son suficientes para colorear cualquier mapa plano (real o imaginario) de manera que regiones que compartan una frontera tengan colores distintos. Este es el mapa que Gardner afirmó que precisaba más de cuatro colores. La solución a este reto, así como la historia de este teorema está muy bien contada aquí por la catedrática de Topología de la UPV-EHU Marta Macho.

Puedes imprimirlo y tratar de colorearlo, aunque, ojo, el hecho de que no lo consigas no será porque Gardner tuviera razón. Su famoso contraejemplo formaba parte de un artículo titulado “Seis descubrimientos sensacionales que por alguna razón han escapado a la atención pública”: una refutación de la teoría de la relatividad, un retrete con cisterna inventado por Leonardo, o una máquina de perpetuo movimiento… publicado el 1 de abril de 1975, vaya, el día de los inocentes del mundo anglosajón.

Así que habrá que revisar las fechas en las que Loyd se atribuyó los inventos de otros, porque lo mismo era bromi.

(La solución al problema de las cuatro fugas es 17 viajes. Puedes consultar la explicación completa en este enlace).

* También puedes seguirnos en Instagram y Flipboard. ¡No te pierdas lo mejor de Verne!